- Tags:: 📜Papers, Demand Forecasting, Forecasting
- Authors: Fotios Petropoulos, Spyros Makridakis, Vassilios Assimakopoulos, Konstantinos Nikolopoulos
- Link:: https://linkinghub.elsevier.com/retrieve/pii/S0377221714001714
- Zotero Link:: petropoulosHorsesCoursesDemand2014
- Source date:: 2014
- Finished date:: 2021-11-01
even today we are unable to answer a very simple question, the one that is always the first tabled during discussions with practitioners: “what is the best method for my data?”
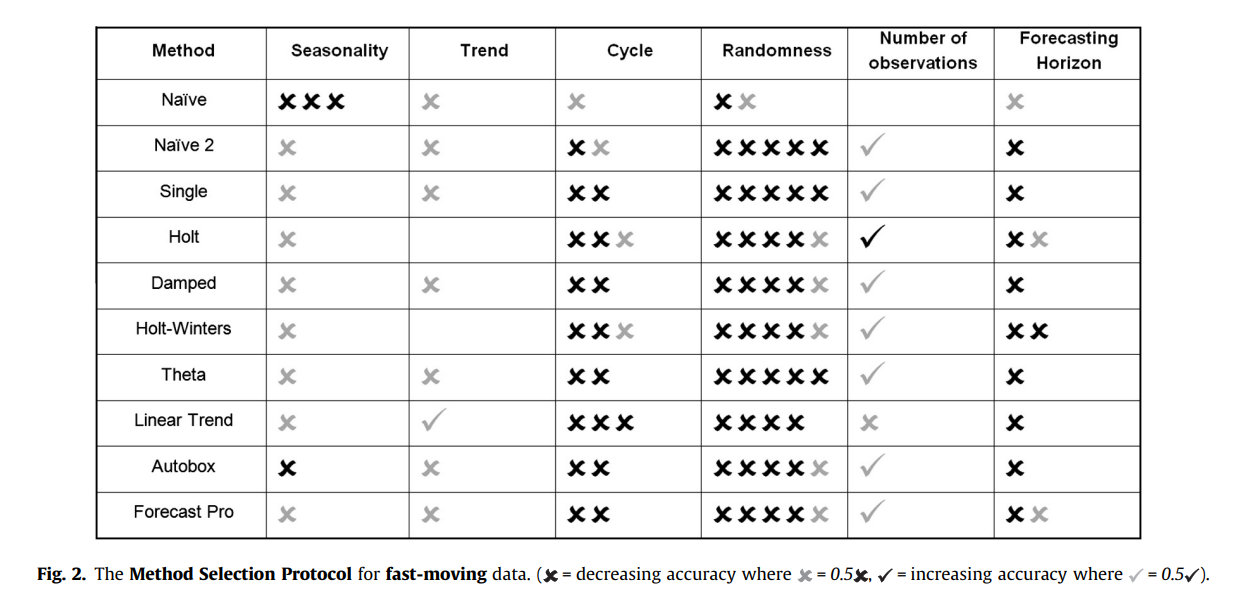
The authors focus on six factors of a time series to compare the performance of different models: seasonality, trend, cycle, randomness, number of observations and forecasting horizon (up to 18 points ahead).. They generate time series with different levels of those factors (combined multiplicatively). It is a pity that they only use single seasonality periods. Results:
- Single Exponential Smoothing, Damped Exponential Smoothing and the Theta method consistently perform better.
- Theta method performs better for longer forecasting horizons, because it accurately predicts the trend in the data
- Combinations of exponential smoothing models have very good performance.
- Randomness is the variable that most affects forecasting accuracy (qué chorprecha!), cycle the next one.
- A true surprise to me:
additional historical information in the form of more observations and lengthier series improves accuracy but to a small extent.
Aplication in real life
They build a regression model (X: the ts factors, Y: the sMAPE), and, since you can estimate the factors of a given ts (via decomposition), you may use the predicted out-of-sample sMAPE as a way to select candidate models for your forecasting (maybe directly picking an ensemble of the 6 best models, as they claim that combinations of large pools of methods is not beneficial).
Other notes
There is a interesting reference to Thinking Fast And Slow, with the same argument Daniel Kahneman makes again in Noise.
the research suggests a surprising conclusion: to maximize predictive accuracy, final decisions should be left to formulas, especially in low-validity environments
The paper also includes simulations on intermittent data, that were not interesting to me at the time.